第1問 次の問い(問1~4)に答えよ。(配点 20)
問1 インターネットを使ったサービス利用に関する次の問い( a・b )に答えよ。
a SNS やメール,Web サイトを利用する際の注意や判断として,適当なものを,次の ~ のうちから二つ選べ。ただし,解答の順序は問わない。 ア イ
⓪相手からのメッセージにはどんなときでも早く返信しなければいけない。
①信頼関係のある相手と SNS やメールでやり取りする際も,悪意を持った者がなりすましている可能性を頭に入れておくべきである。
②Web ページに匿名で投稿した場合は,本人が特定されることはない。
③SNS の非公開グループでは,どんなグループであっても,個人情報を書き込んでも問題はない。
④一般によく知られているアニメのキャラクターの画像を SNS のプロフィール画像に許可なく掲載することは,著作権の侵害にあたる。
⑤芸能人は多くの人に知られていることから肖像権の対象外となるため,芸能人の写真を SNS に掲載してもよい
b インターネット上の情報の信ぴょう性を確かめる方法として,最も適当なものを次の ⓪~③ のうちから一つ選べ。
⓪検索エンジンの検索結果で,上位に表示されているかどうかで判断する。
①Q&A サイトの回答は,多くの人に支持されているベストアンサーに選ばれているかどうかで判断する。
②SNS に投稿された情報は,共有や「いいね」の数が多いかどうかで判断する。
③特定の Web サイトだけでなく,書籍や複数の Web サイトなどを確認し,比較・検証してから判断する
~中略~
問3 次の文章を読み,空欄 カ~ク に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
基本的な論理回路には,論理積回路(AND 回路),論理和回路(OR 回路),否定回路(NOT 回路)の三つがあげられる。これらの図記号と真理値表は次の表1で示される。真理値表とは,入力と出力の関係を示した表である。
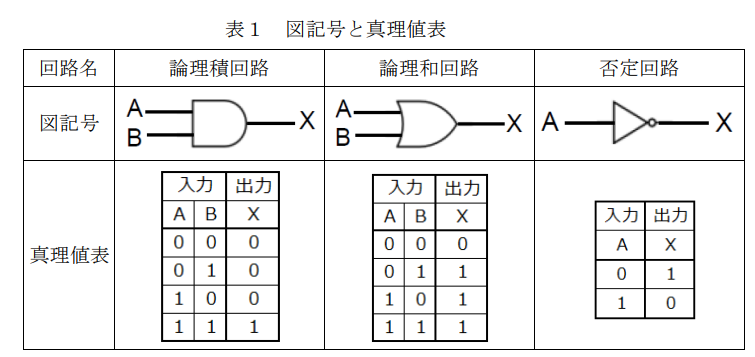
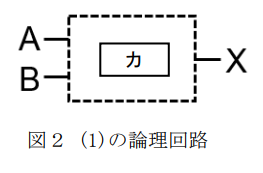
(1) S航空会社が所有する旅客機の後方には,トイレが二つ(A・B)ある。トイレ A とトイレ B の両方が同時に使用中になると乗客の座席前にあるパネルのランプが点灯し,乗客にトイレが満室であることを知らせる。入力 A は,トイレ A が使用中の場合には1,空いている場合には0とする。B についても同様である。出力 X はランプが点灯する場合に1,点灯しない場合に0となる。これを実現する論理回路は次の図2である
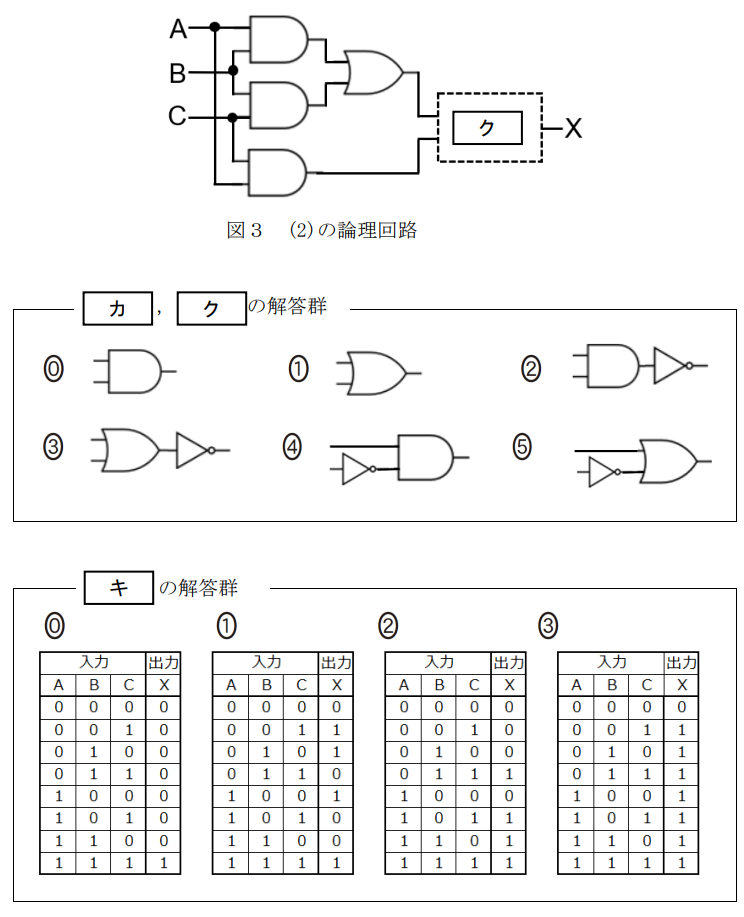
(2) S航空会社では新しい旅客機を購入することにした。この旅客機では,トイレを三つ(A・B・C)に増やし,三つのうちどれか二つ以上が使用中になったら混雑を知らせるランプを点灯させる。入力や出力は(1)と同様とする。
この場合の真理値表は で,これを実現する論理回路は図3である
~中略~
~中略~
問3 太郎さんは,先生から二次元コードを作成することができる図4のようなWeb アプリケーションを教えてもらった。この二次元コード画像作成ツールは,二次元コード化する文字列とセルのサイズ(大きさ),誤り訂正のレベル(復元
能力),画像ファイル形式を指定すると二次元コードの画像が作成できるものであった。
下線部Bについて,興味を持った太郎さんは,この作成ツールを使い,二次元コード化する文字列の長さと誤り訂正のレベルによってどのようにセルの縦と横の数が変化するか調べることにした。そこで,試しに英小文字(a~z)で構成する文字列の文字数をいろいろ変えて二次元コードを作成したところ,表1のようになった。表中の n×n はそれぞれセルの縦と横の数を表している。
なお,この作成ツールではセルの縦と横の数は自動的に最適な数に調整される。また,復元能力の値(%)が大きいほど誤りを訂正する能力が高いことを表し,例えば,復元能力 30%は,二次元コードの面積の最大 30%が読み取れなくてもデータを復元できることを意味する。

~中略~
B 次の文章を読み,後の問い(問1~3)に答えよ。
Mさんのクラスでは,文化祭の期間中2日間の日程でクレープを販売することにした。
1日目は,慣れないこともあり,客を待たせることが多かった。そこで,1日目が終わったところで,調理の手順を見直すなど改善した場合に,どのように待ち状況が変化す
るかシミュレーションすることにした。なお,このお店では同時に一人の客しか対応できないとし,客が注文できるクレープは一枚のみと考える。また,注文は前の客に商品
を渡してから次の注文を聞くとして考える。
問1 次の文章および表中の空欄 ~ に当てはまる数字をマークせよ。
まず,Mさんは,1日目の記録を分析したところ,注文から商品を渡すまでの一人の客への対応時間に約4分を要していることが分かった。
次に,クラスの記録係が1日目の来客時刻を記録していたので,最初の 50 人の客の到着間隔を調べたところ,表1の人数のようになった。この人数から相対度数を求め,その累積相対度数を確率とみなして考えてみた。また,到着間隔は一定の範囲をもとに集計しているため,各範囲に対して階級値で考えることにした。
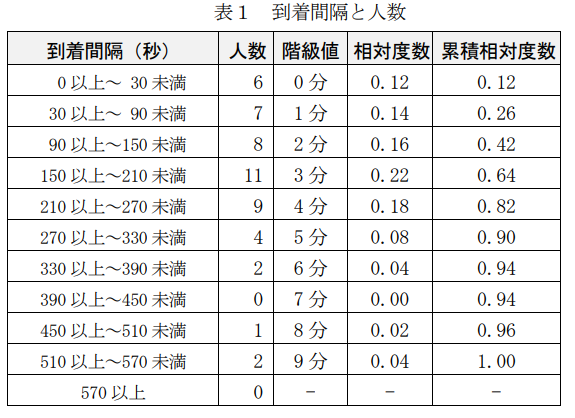
そして,表計算ソフトウェアで生成させた乱数(0 以上 1 未満の数値が同じ確率で出現する一様乱数)を用いて試しに最初の 10 人の到着間隔を,この表1をもとに導き出したところ,次の表2のようになった。ここでの到着間隔は表1の階級値をもとにしている。なお,1人目は到着間隔0分とした。
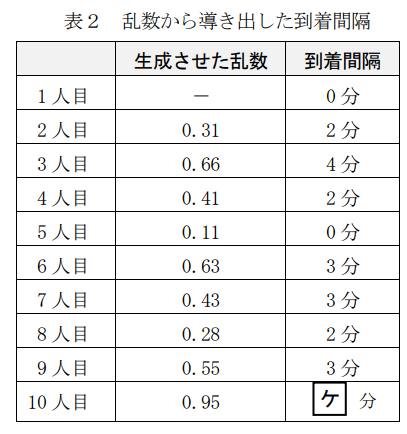
表2の結果から 10 人の客の待ち状況が分かるように,次の図1のように表してみることにした(図1は6人目まで記入)。ここで,待ち時間とは,並び始めてから直前の人の対応時間が終わるまでの時間であり,対応時間中の客は待っている人数に入れないとする。このとき,最も待ち人数が多いときは 人であり(これを最大待ち人数という),客の中で最も待ち時間が長いのは 分であった。
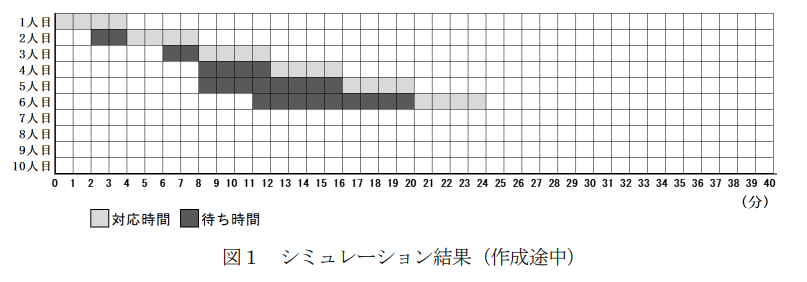
問2 図1の結果は,客が 10 人のときであったので,Mさんは,もっと多くの客が来た場合の待ち状況がどのようになるか知りたいと考えた。そこでMさんは,客が10人,20 人,30 人,40 人来客した場合のシミュレーションをそれぞれ 100 回ずつ行ってみた。次の図2は,それぞれ 100 回のシミュレーションでの最大待ち人数の頻度を表したものである。
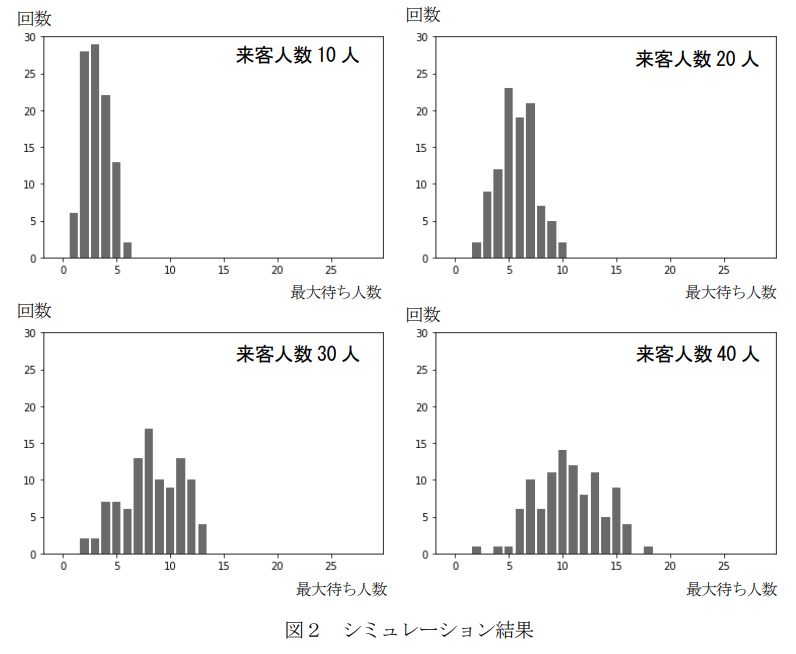
~中略~
問2 次の文章の空欄 ~ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
S:まずは,関数「枚数(金額)」のプログラムを作るために,与えられた金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみます。もう少しヒントが欲しいなぁ。
T:金額に対して,高額の硬貨から使うように考えて枚数と残金を計算していくとよいでしょう。また,金額に対して,ある額の硬貨が何枚まで使えて,
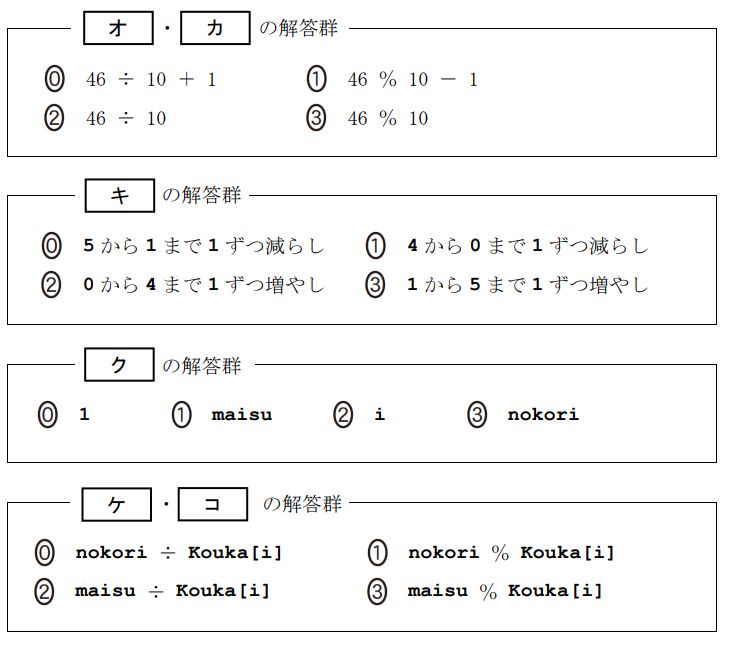
残金がいくらになるかを計算するには,整数値の商を求める演算『÷』とその余りを求める演算『%』が使えるでしょう。例えば,46 円に対して 10円玉が何枚まで使えるかは で,その際にいくら残るかはで求めることができますね。
S:なるほど!あとは自分でできそうです。
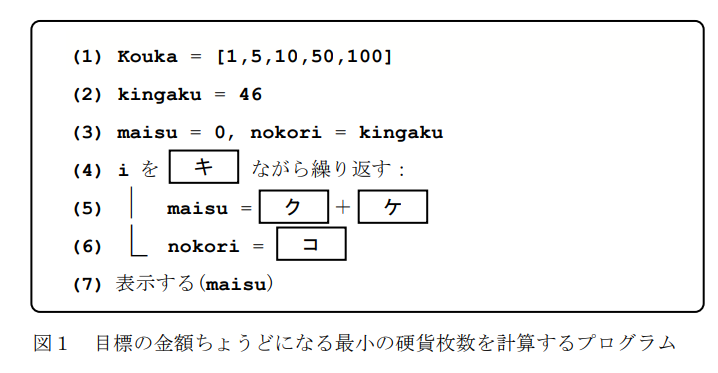
Sさんは,先生(T)との会話からヒントを得て,変数 kingaku に与えられた目標の金額(100 円以下)に対し,その金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみた(図1)。ここでは例として目標の金額を 46
円としている。
配列 Kouka に硬貨の額を低い順に設定している。なお,配列の添字は 0 から始まるものとする。最低額の硬貨が 1 円玉なので Kouka[0]の値は 1 となる。
先生(T)のヒントに従い,高額の硬貨から何枚まで使えるかを計算する方針で,(4)~(6)行目のような繰返し文にした。この繰返しで,変数 maisu に支払いに使う硬貨の枚数の合計が計算され,変数 nokori に残りいくら支払えばよいか,という残金が計算される。
実行してみると が表示されたので,正しく計算できていることが分かる。いろいろな例で試してみたが,すべて正しく計算できていることを確認できた。
~中略~


コメント